The Random-Greedy Path¶
For large and complex contractions the exhaustive approaches will be too slow
while the greedy path might be very far from optimal. In this case you might
want to consider the 'random-greedy' path optimizer. This samples many
greedy paths and selects the best one found, which can often be exponentially
better than the average.
import opt_einsum as oe
import numpy as np
import math
eq, shapes = oe.helpers.rand_equation(40, 5, seed=1, d_max=2)
arrays = list(map(np.ones, shapes))
path_greedy = oe.contract_path(eq, *arrays, optimize='greedy')[1]
print(math.log2(path_greedy.opt_cost))
# 36.04683022558587
path_rand_greedy = oe.contract_path(eq, *arrays, optimize='random-greedy')[1]
print(math.log2(path_rand_greedy.opt_cost))
# 32.203616699170865
So here the random-greedy approach has found a path about
16 times quicker (= 2^(36 - 32)).
This approach works by randomly choosing from the best n contractions at
each step, weighted by a
Boltzmann factor with
respect to the contraction with the ‘best’ cost. As such, contractions with
very similar costs will be explored with equal probability, whereas those with
higher costs will be less likely, but still possible. In this way, the
optimizer can randomly explore the huge space of possible paths, but in a
guided manner.
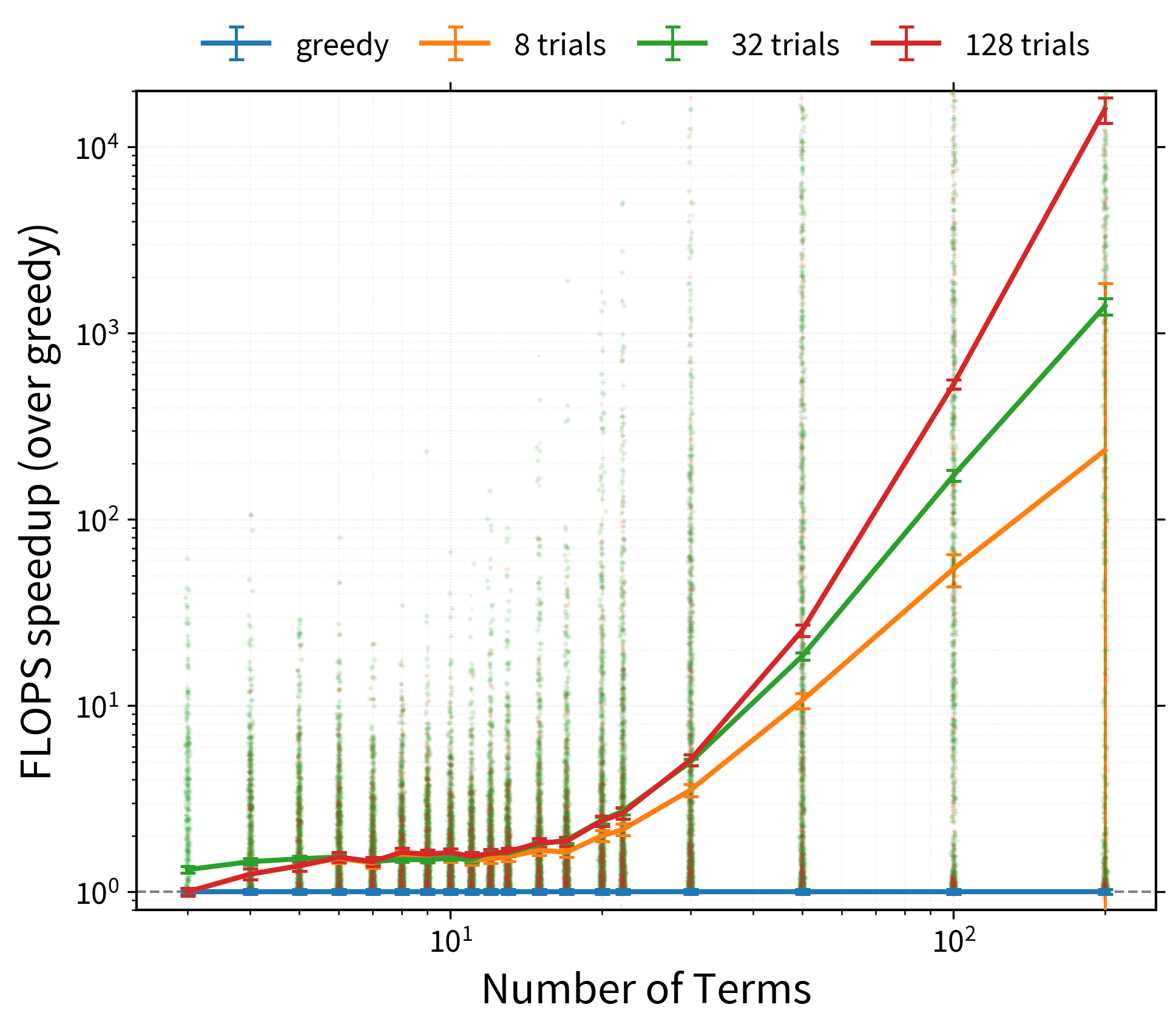
The following graph roughly demonstrates the potential benefits of the
'random-greedy' algorithm, here for large randomly generated contractions,
with either 8, 32 (the default), or 128 repeats:
Note
Bear in mind that such speed-ups are not guaranteed - it very much depends on how structured or complex your contractions are.
Customizing the Random-Greedy Path¶
The random-greedy optimizer can be customized by instantiating your own
RandomGreedy object. Here you can control:
temperature- how far to stray from the locally ‘best’ contractionsrel_temperature- whether to normalize the temperaturenbranch- how many contractions (branches) to consider at each stepcost_fn- how to cost potential contractions
There are also the main RandomOptimizer
options:
max_repeats- the maximum number of repeatsmax_time- the maximum amount of time to run for (in seconds)minimize- whether to minimize for total'flops'or'size'of the largest intermediate
For example, here we’ll create an optimizer, then change its temperature
whilst reusing it. We’ll also set a high max_repeats and instead use a
maximum time to terminate the search:
optimizer = oe.RandomGreedy(max_time=2, max_repeats=1_000_000)
for T in [1000, 100, 10, 1, 0.1]:
optimizer.temperature = T
path_rand_greedy = oe.contract_path(eq, *arrays, optimize=optimizer)[1]
print(math.log2(optimizer.best['flops']))
# 32.81709395639357
# 32.67625007170783
# 31.719756871539033
# 31.62043317835677
# 31.253305891247
print(len(optimizer.costs)) # the total number of trials so far
# 2555
So we have improved a bit on the standard 'random-greedy' (which does 32
repeats by default). The optimizer object now stores both the best path
found so far - optimizer.path - as well as the list of flop-costs and
maximum sizes found for each trial - optimizer.costs and
optimizer.sizes respectively.
Parallelizing the Random-Greedy Search¶
Since each greedy attempt is independent, the random-greedy approach is
naturally suited to parallelization. This can be automatically handled by
specifying the parallel keyword like so:
# use same number of processes as cores
optimizer = oe.RandomGreedy(parallel=True)
# or use specific number of processes
optimizer = oe.RandomGreedy(parallel=4)
Warning
The pool-executor used to perform this parallelization is the
ProcessPoolExecutor from the concurrent.futures
module. This
is only part of the standard library in Python 3. For Python 2 consider
installing the
backport of this module or see below.
For full control over the parallelization you can supply any pool-executor like object, which should have an API matching the Python 3 concurrent.futures module:
from concurrent.futures import ProcessPoolExecutor
pool = ProcessPoolExecutor()
optimizer = oe.RandomGreedy(parallel=pool, max_repeats=128)
path_rand_greedy = oe.contract_path(eq, *arrays, optimize=optimizer)[1]
print(math.log2(optimizer.best['flops']))
# 31.64992600300931
Other examples of such pools include: